Ferenc Kun
professor, Department of Theoretical Physics, University of Debrecen

Fragmentation Phase Transition

Fragmentation, i.e. the breaking of particulate materials into a large number of smaller pieces is abundant in nature and underlies several industrial processes, which attracted a continuous interest in scientific research over the past decades. Fragmentation phenomena can be observed on a broad range of length scales from the collisional evolution of asteroids and meteor impacts on the astrophysical scale, through geological phenomena and industrial applications on the intermediate scale down to the break-up of large molecules and heavy nuclei on the atomic scale. In laboratory experiments on the fragmentation of solids, the energy input is usually achieved by shooting a projectile into a solid block, making an explosion inside the sample or by the collision of macroscopic bodies (free fall impact).

The most striking observation on fragmentation is that the distribution of fragment sizes or masses shows a power law behavior, independently on the way of imparting energy, relevant microscopic interactions and length scales involved. For heterogeneous brittle materials experiments revealed that the exponent of the fragment mass distribution is mainly determined by the dimensionality of the system. The understanding of this observed universality of fragmentation phenomena is till today the main driving force of theoretical studies.

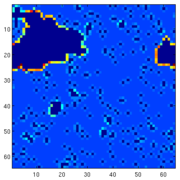
Collision of two brittle discs Collision of two discs generated by computer simulations. The discs have a heterogeneous microstructure and a highly brittle mechanical response. Close to the impact site all fragments are very small, since here the two bodies are completely shattered. Big fragments are formed by cracks which reach the surface of the bodies opposite to the impact site.

Simulating the collision of two-dimensional disordered solid objects, we have shown that depending on the imparted energy, the collision has two different outcomes: the final state of the solids can be damaged or fragmented with a sharp transition in between at a critical energy. Analyzing the energetics of the collision process and the fragment mass distributions in the final state we found that the transition between the damaged and fragmented states occurs analogously to continuous phase transitions [36]. We concluded that the universal fragment mass distributions observed experimentally are the consequence of the underlying phase transition. Later on experiments confirmed our theoretical findings. The publication presenting the fragmentation phase transition was selected by Physical Review Focus.